-
32 000 руб.
-
6 900 руб.
-
11 000 руб.
-
15 000 руб.
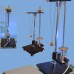
Универсальный маятник. ФМ-13
Описание
Маятник универсальный
Лабораторная установка обеспечивает возможность изучения законов колебания математического и физического (оборотного) маятников. Установка позволяет экспериментально определить ускорение силы тяжести методами математического и физического маятников, а также центр масс физического маятника.
Установка состоит из математического маятника (бифилярный подвес) и физического маятника (жесткий металлический стержень с рисками через каждые 10 мм для отсчета длины, две призматические опоры, два груза с возможностью перемещения и фиксации по всей длине стержня), которые устанавливаются на кронштейне, закрепленном на верхнем конце стойки. Стойка установлена на основании. На стойке нанесена миллиметровая шкала. В нижней части стойки крепится кронштейн с фотодатчиком.
Технические характеристики:
| Максимальная длина математического маятника, мм | 385±1 |
| Длина стержня физического (оборотного) маятника, мм | 440±1,5 |
| Масса физического (оборотного) маятника, кг | 1,05±0,1 |
| Измеряемое количество колебаний любого из маятников, не более | 99 |
| Диапазон измерения миллиметровой шкалы вертикальной стойки, мм | 50...400 |
| Цена деления шкалы, мм | 1±0,1 |
| Измерение интервалов времени осуществляется в диапазоне, с | 0,01...99,99 |
| Питание установки осуществляется от сети переменного тока | 220В, 50Гц |
| Потребляемая мощность, ВА, не более | 50 |
| Габаритные размеры, мм, не более | 250х210х560 |
| Масса, кг, не более | 5 |
в комплетк входит секундомер электронный ФМ-1/1
Лабораторная работа
ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ математического МАЯТНИКА
Цель работы: Экспериментальная проверка закономерностей движения математического маятника.
Содержание работы
Математическим маятником обычно называют тело малых размеров (материальную точку), подвешенное к неподвижной точке на невесомой нерастяжимой нити и совершающее движение в вертикальной плоскости под действием силы тяжести (рис. 1.1). В полярных координатах уравнение движения такой системы имеет вид:
, или , где .
Д
д
для малых углов отклонения маятника, при которых , оно сводится к уравнению гармонических колебаний.
Решение данного уравнения может быть записано в виде ,
где A – амплитуда, – начальная фаза колебания. Таким образом, при малых амплитудах математический маятник совершает гармонические колебания с частотой и периодом .
Схема установки показана В качестве математического маятника используется металлический шар, подвешенный на двух капроновых нитях к кронштейну . На этом же кронштейне находится также ролик.
позволяющий изменять длину подвески. На нижнем кронштейне укреплен фотодатчик . Расстояние между кронштейнами определяется по нанесенной на штатив шкале
Выполнение работы
1. Установить нижний кронштейн с фотодатчиком в крайнее нижнее положение шкалы так, чтобы верхняя плоскость кронштейна совпала с одной из рисок шкалы. Установить верхний кронштейн таким образом, чтобы шарик математического маятника оказался в рабочей зоне фотодатчика. Вращая ролик, добиться такого положения шарика, при котором его центральная риска будет совпадать по высоте с риской на фотодатчике. По шкале на вертикальной стойке определить длину математического маятника ll.
2. Привести математический маятник в колебательное движение, отклонив металлический шарик на угол 5 – 6 градусов, после чего нажать на кнопку СБРОС на блоке. По показанию таймера определить значение времени 40 … 50 колебаний маятника. Определить среднее значение периода колебаний маятника по формуле , где tl – время колебаний, N – число колебаний.
3. Передвинуть вверх кронштейн с фотодатчиком на два деления шкалы вертикальной стойки. Вращая ролик добиться такого положения шарика, при котором его центральная риска будет совпадать по высоте с риской на фотодатчике. По шкале вертикальной стойки определить длину математического маятника l2. Повторить эксперимент
4. Повторить эксперимен, уменьшая длину маятника, 5-6 раз.
5. Построить график зависимости квадрата периода колебаний от длины маятника. Аппроксимировать полученную зависимость прямой линией . Определить коэффициент наклона a по методу наименьших квадратов (см. Приложение). Найти величину ускорения свободного падения .
6. Сравнивая теоретическое и экспериментальное значения ускорения свободного падения, определить относительную погрешность по формуле